Guía para ver los montes de África desde Málaga
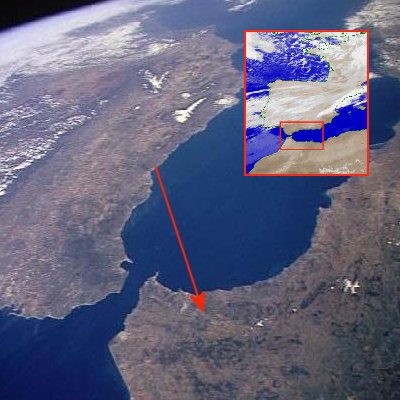

¡Mira!¡Se ven los montes de África!
Seguramente, seremos muchos los malagueños que hemos dicho algo parecido
cuando, los días de mucha claridad, se divisan en el horizonte algunas
de las montañas más altas del Rif, en África. Pero para verlas, hay que estar al menos
a unas decenas de metros de altura, ya que, desde la misma playa malagueña, es realmente
difícil divisar alguna de las cumbres rifeñas. La curvatura de la Tierra lo impide.
Y es que, aunque no lo parezca, la esfericidad del planeta es evidente a simple vista.
Por su "culpa", el horizonte visible en el mar para un observador situado en la playa
apenas alcanza seis o siete kilómetros. Para este mismo observador, el horizonte, o sea, el mar, tapará gran parte
del casco de cualquier barco situado a más de 12 kilómetros de distancia, y prácticamente
ocultará cualquier montaña de 2000 metros situada a 200 kilómetros de distancia.
Este fue precisamente el principal argumento de Aristóteles para defender que
la Tierra es redonda.
El caso es que tengo la fortuna de vivir en un lugar privilegiado desde el cual puedo divisar
los montes de África casi cualquier día despejado de invierno, e incluso alguna vez, con la
ayuda del potente telescopio de mi amigo Angel, he divisado las luces de alguna aldea en la falda del
monte más alto de todos los que se divisan. Así que, picado por la curiosidad, me pregunté
cual sería el nombre de aquel imponente cerro y de aquella diminuta aldea.
Y esta es la historia...
El mapa
Acudí a un atlas e inmediatamente deduje que el misterioso monte debía ser el
Tidighine,
la cumbre más alta del Rif, situada a 208 kilómetros de Málaga en línea recta, prácticamente en dirección sur
(a 184º de azimuth, exactamente)
(como veremos más abajo, estaba equivocado...)
El siguiente formulario permite conocer el azimuth y la distancia entre dos puntos,
a partir de sus coordenadas geográficas.
Si conoces las coordenadas sólo en formato UTM, entonces pulsa esto para convertirlas
La brújula
El monte Tidighine tiene una altura de 2456 metros sobre el nivel del mar, muy por encima del
resto de la cordillera. Por su dimensión y relativa proximidad pensé: ¡no puede ser otro! Sin embargo, la brújula me decía lo contrario. El monte que parece más alto desde
Málaga está bastante más a poniente (a 209º más o menos, en el lado derecho de esta laaaaarga foto).
Cada marca de la escala, de izquierda a derecha, representa un grado, y unos tres kilómetros de la costa africana (como el paseo marítimo, más o menos).

Había otros candidatos, pero sólo uno en la dirección adecuada: el
Kelti,
situado a mucha
menos distancia (173 kilómetros), pero que también es bastante más bajo, pues sólo tiene
1928 metros de altitud. En la siguiente figura se ve al Kelti (con la etiqueta 2A, al centro, a la izquierda) en un mapa del norte de Marruecos, donde se han marcado algunos otros montes y lugares de interés, así como sus altitudes (verde), distancias a Málaga (amarillo), y azimuths (celeste)correspondientes a mi punto de observación.
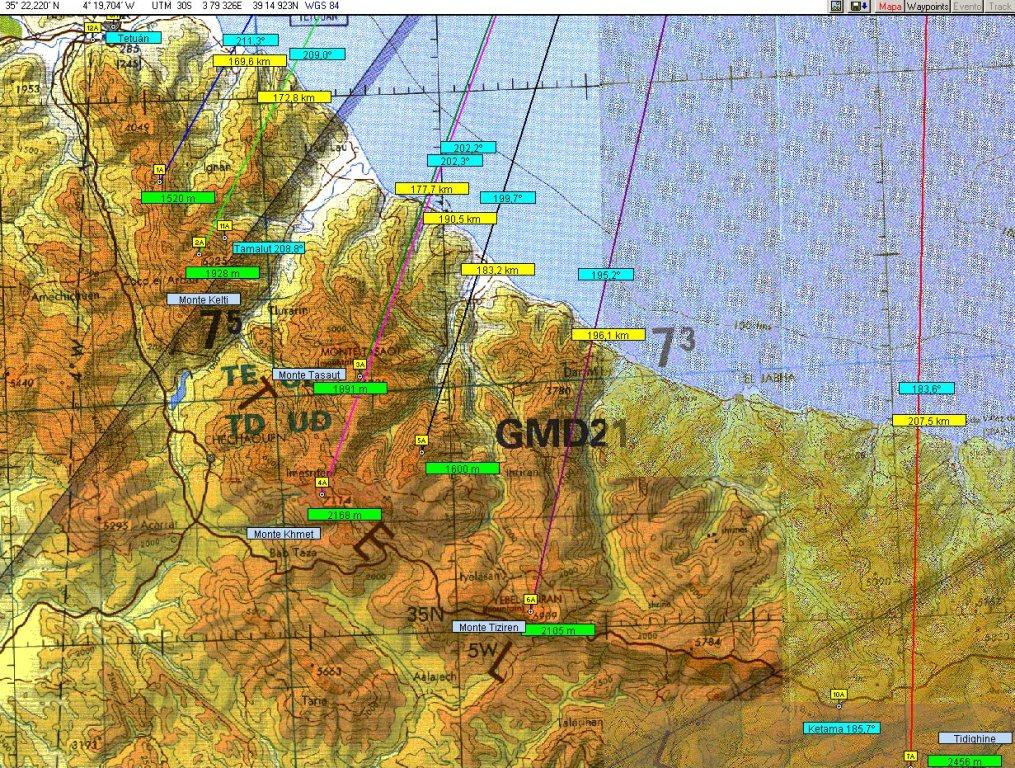
El único inconveniente para que el Kelti fuera el "elegido" es que, al hacer los cálculos, la menor distancia del Kelti a Málaga no era suficiente para que éste pudiera aparentar más altitud que el Tidighine, pero en mis estimaciones iniciales había olvidado un aspecto importantísimo:
La curvatura terrestre
¡Al estar más cerca, y debido a que la Tierra es redonda,
el Kelti debe parecer algo más alto en relación al Tidighine, ! Pero...¿cuánto?
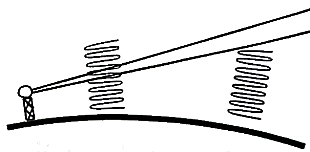
Saqué mis apuntes de trigonometría del baúl, hice algunos cálculos y... ¡¡Sorpresa: prácticamente NINGUNO de los montes
de África es visible desde mi observatorio, emplazado a 55 metros sobre el nivel del mar!! ¿Qué es lo que falla? Veamos; lo cierto es que los cálculos eran correctos, pero había olvidado otro aspecto: la refracción de la luz en la
atmósfera.
La luz se dobla
La refracción es el fenómeno responsable de los espejismos. Hace que la luz siga una trayectoria curva, más pronunciada cuando sigue un recorrido cercano a la superficie. Ya había leído, hace algún tiempo, en
un interesante libro ("A ras del cielo", de David Galadí-Enríquez) que cuando vemos una puesta de sol, en realidad, el sol ya
se puso unos segundos antes.

Este fenómeno varía según las condiciones atmosféricas, pero éstas se pueden tener fácilmente en cuenta,
con un formulario como este:
(Si te ha resultado interesante, escríbeme y cuéntamelo;-)
Esta web fue creada entre el 26 y el 29 de diciembre de 2003.
El 6 de enero de 2006, un día de excepcional visibilidad, alcancé a ver el Monte Tidighine. El video se puede consultar en este sitio .
También en enero, pero de 2015, Juan Strafford me envió este video tomado desde el Mirador de la Viborilla, en Benalmádena (a 6 metros sobre el nivel del mar!), en el que se puede observar el Tidighine. Adjunto también algunas fotos en alta resolución de Juan:





